dg4est

My primary research revolves around developing high-fidelity numerical methods for Computational Fluid Dynamics problems with applications to Wind Energy and Aerospace. This involves principally writing code de novo as the problems we target require leadership-class supercomputing capabilities. My research vision is to develop highly-scalable and highly-efficient algorithms coupling scientific computation with data-informed modeling suitable for leadership-class heterogeneous supercomputers and to facilitate industry-ready engineering simulations tools applicable to the fields of aerospace and renewable energy.

The primary software I’ve developed over the past five years in dg4est which is a discontinuous Galerkin method leveraging the p4est framework for managing and adapting the grid topology. dg4est is the primary off-body CFD solver within the WAKE3D framework and has been utilized in many applications. Some of the features of dg4est are outlined here.

2D and 3D Simulations
- Cartesian and unstructured (high-order curvilinear) quad/hex meshes
- gmsh mesh reader (binary, ascii): 2.X, 4.X formats
- Dynamic adaptive mesh refinement (non-conforming) with p4est
High-Order Spatial Discretizations: Discontinous Galerkin
- Nodal tensor-product basis functions: Lagrange polynomials (up to 24th order)
- Modal tensor-product basis functions: Legendre polynomials
- Quadrature Integration (collocation/over-integrable): Gauss-Legendre (2p+1 accuracy), Lobatto-Gauss (2p-1 accuracy)
- Kinetic energy-preserving scheme based on flux differencing: Pirozzoli, Kennedy & Gruber
- Riemann solvers: Lax Friedrichs, Roe (with entropy fix)
- Diffusion solvers: SIP, BR2
- Governing equations
  - compressible Euler equations (inviscid)
  - compressible Navier-Stokes equations (viscous)
- LES subgrid-scale models
  - constant Smagorinsky
  - dynamic Smagorinksy
  - WALE
- Sources: gravity, Coriolis
- Boundary conditions: free-stream, slip wall (symmetry), non-slip wall, characteristic, total inlet, static pressure outlet, periodic
High-Order Temporal Discretizations
- Explicit Time Stepping
  - RK1: Forward Euler
  - RK2: SSP (strong-stability preserving)
  - RK3: SSP
  - RK4: 3/8-rule
- Implicit Time Stepping (dual time stepping: RK-optimized smoothers)
  - BDF-1
  - BDF-2
  - Space-Time DG (up to 10th order)
  - Preconditioned FIRK 2-stage Gauss-Legendre
  - Preconditioned FIRK 2-stage Radau IIA
p-Multigrid Solution Convergence Acceleration (space-time, implicit, steady-state)
- Full Approximation Scheme (FAS)
- V-/F-/W-Cycling
Acoustic Analysis
- Ffowcs-Williams Hawkings (FW-H) acoustic-analogy formulation
Overset Simulation Infrastructure
- TIOGA interface
In-situ Data Extraction
- points, lines, planes, volumes
- VisIt Libsim tnterface
- SENSEI interface
VTK Visualization
- parallel VTU format (VisIt, paraview)
- High-order VTK Lagrange format (paraview)
Post-processing
- LES SGS TKE
- Temporal statistics: mean, standard deviation, 95% confidence interval
- Reynolds stresses
- Proper Orthogonal Decomposition (POD)/Principal Component Analysis (PCA)
- MPI wall-clock time histogram viewer
- Analytical spatial error calculator (order of accuracy verification)
Unit Testing (gtest framework) and Regresion Testing

Future Developments

Release the code as open source via GitHub!
GPU Implementation using OCCA: NVIDIA, AMD, Intel hardware
- Full GPU offload including AMR (dynamic)
Mixed-element meshes (with AMR): tets, pyramids, prisms, hexes
Boundary Representation (brep) incorporation for curved-mesh adaption
Wall-Modeled Large Eddy Simulation

Unstructured High-Order Geometry

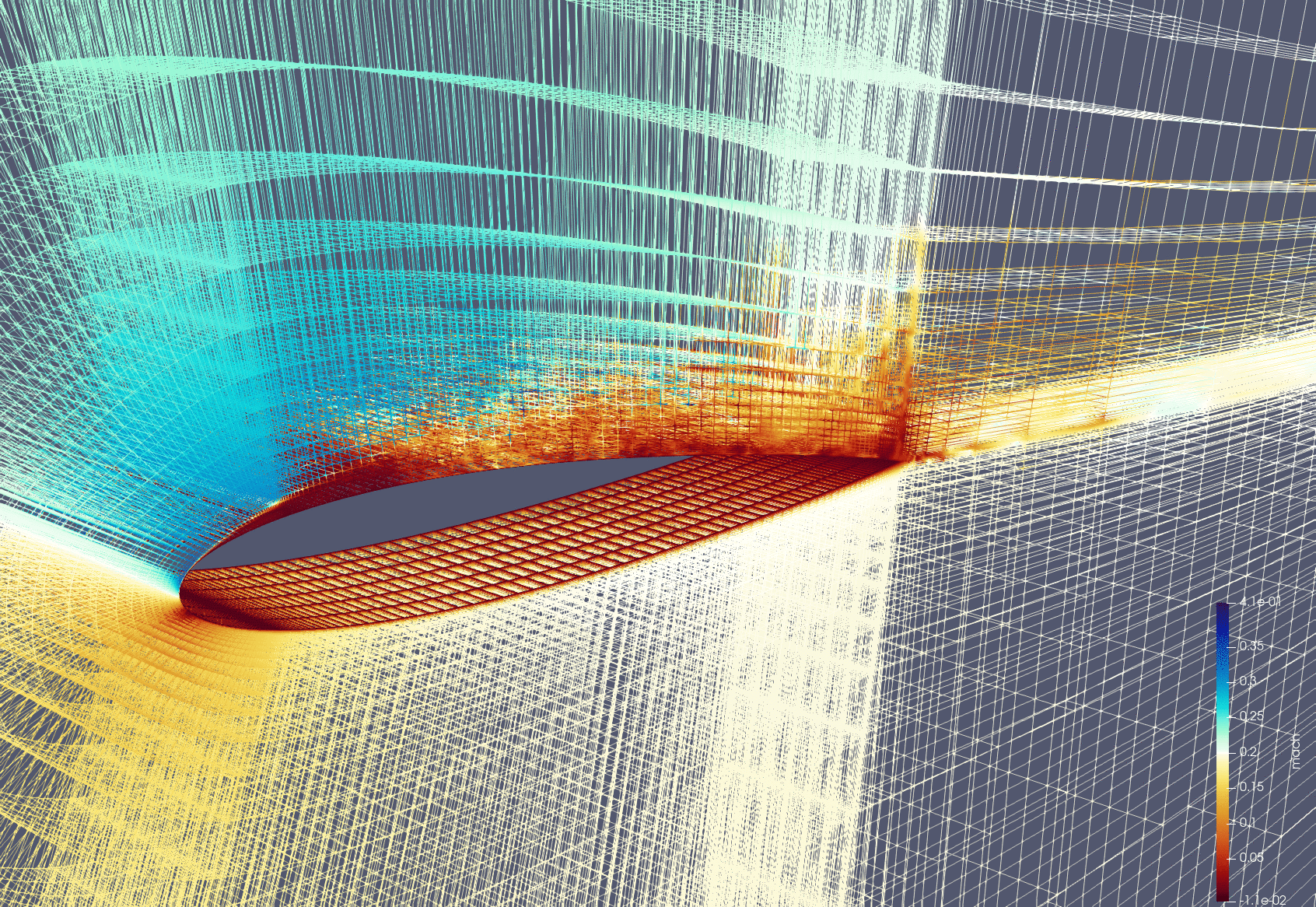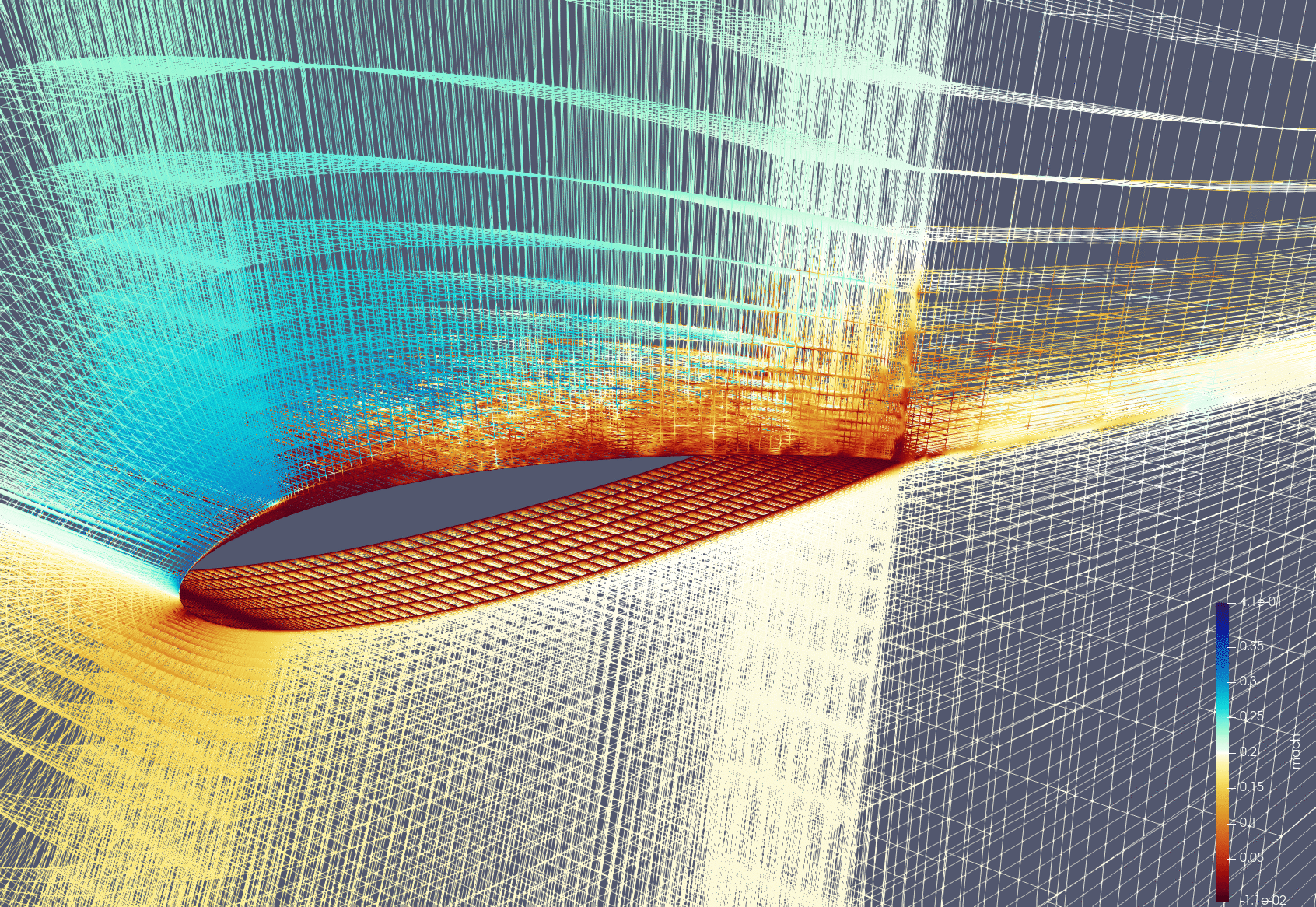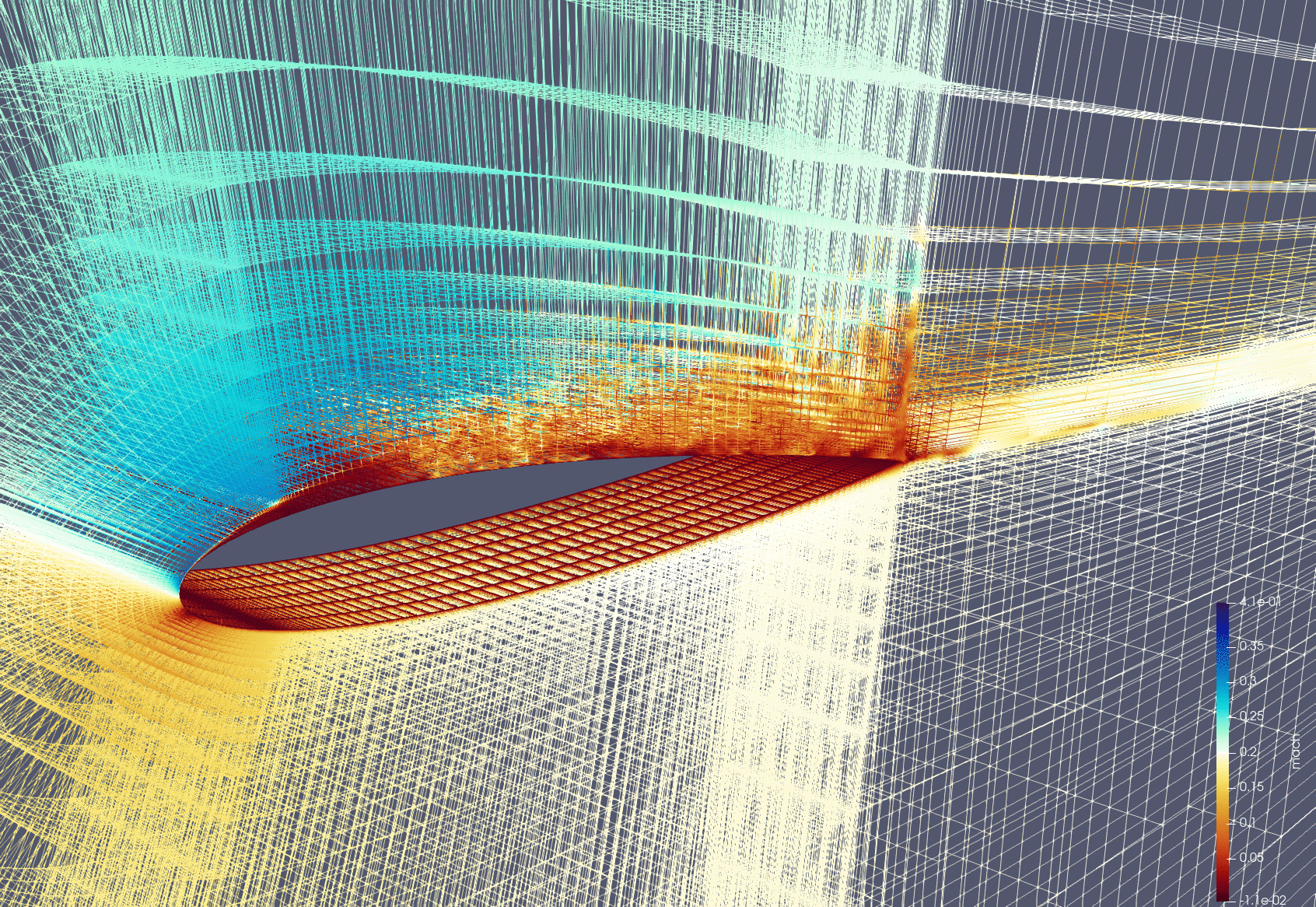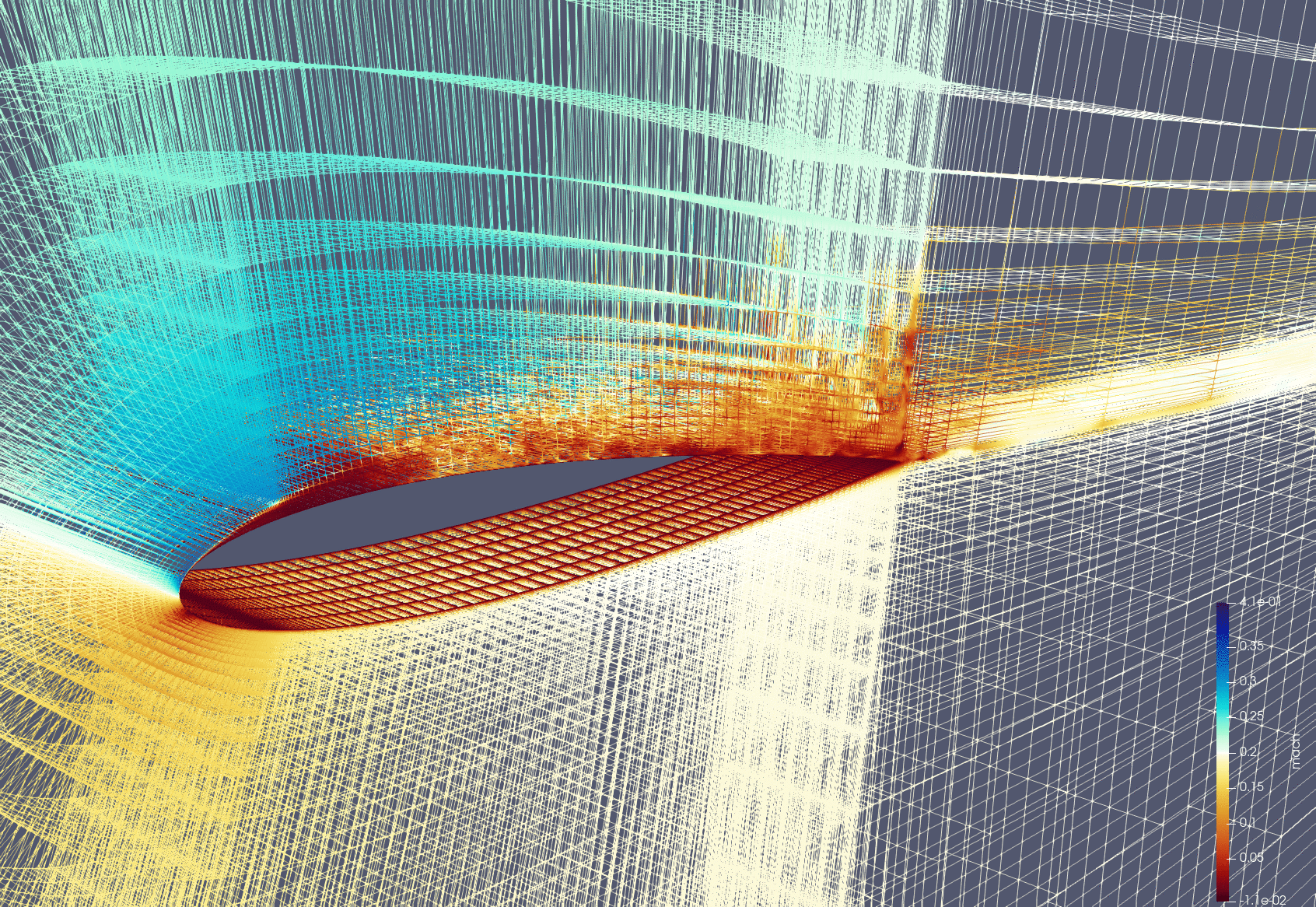
Adaptive Mesh Refinement

Adaptive mesh refinement allows for long turbulent wake tracking as illustrated in this flow over a sphere.

CartDG

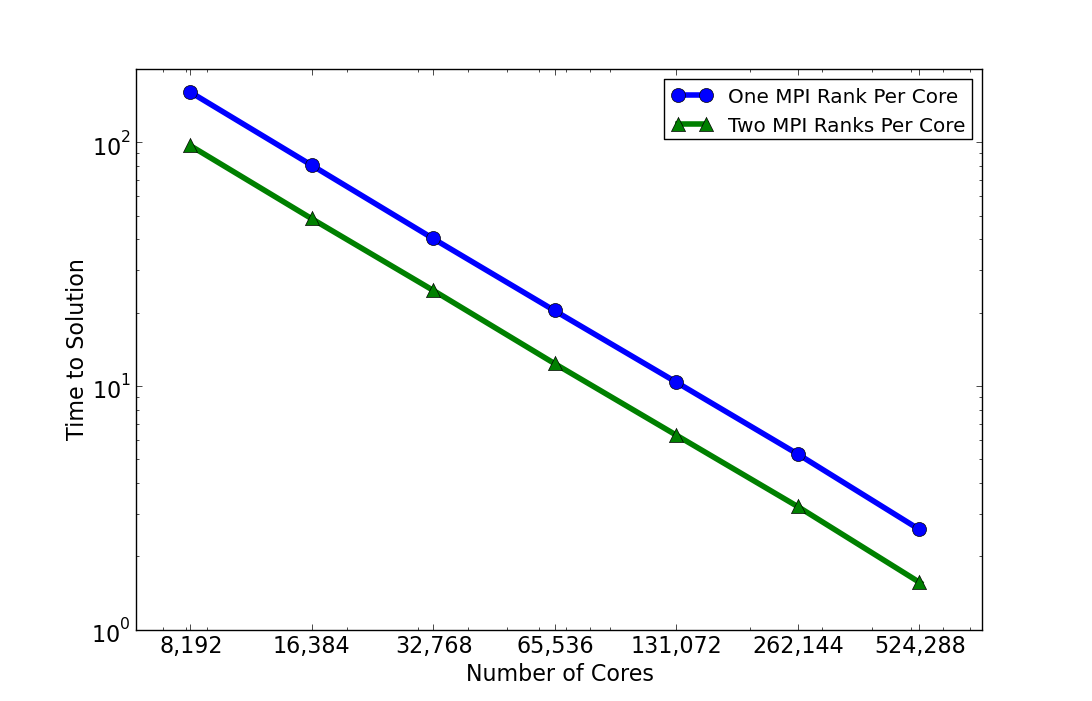
dg4est utilizes a varible order hp discontinuous Galerkin implementation. The numerical FEM kernels in dg4est are carried over from my purely Cartesian DG solver known as CartDG. CartDG discretizes the compressible Navier–Stokes equations with Coriolis and gravitational forces. There are options for a constant or dynamic Smagorinsky Subgrid-Scale (SGS) Large Eddy Simulation (LES) model. The solver itself is designed for computational efficiency on Cartesian meshes and has been strong scaled to over 1 million MPI ranks on Argonne National Laboratory’s Mira Supercomputer as seen below.

Strong scaling of the CartDG DG solver on Argonne's Mira supercomputer on over 1 million MPI ranks.

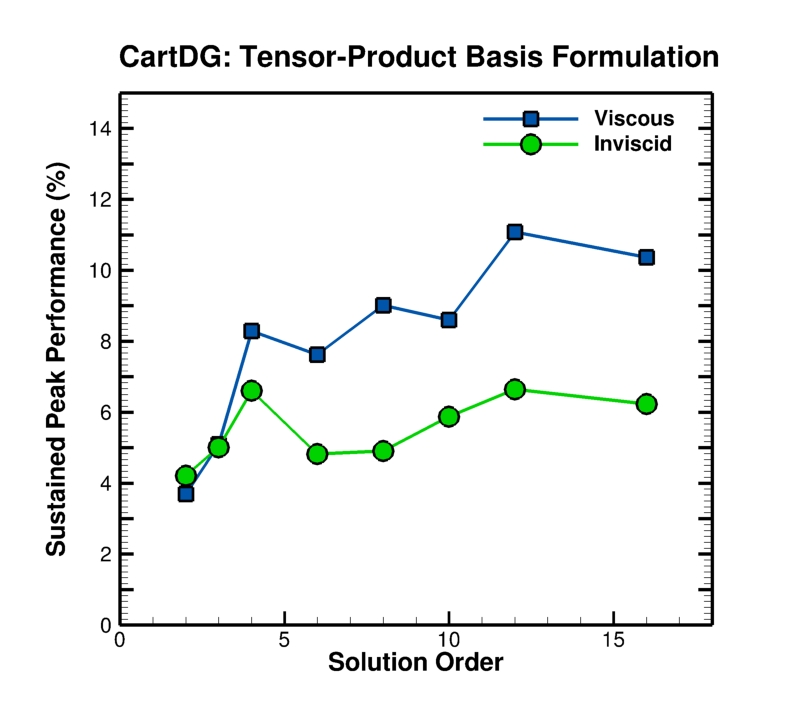
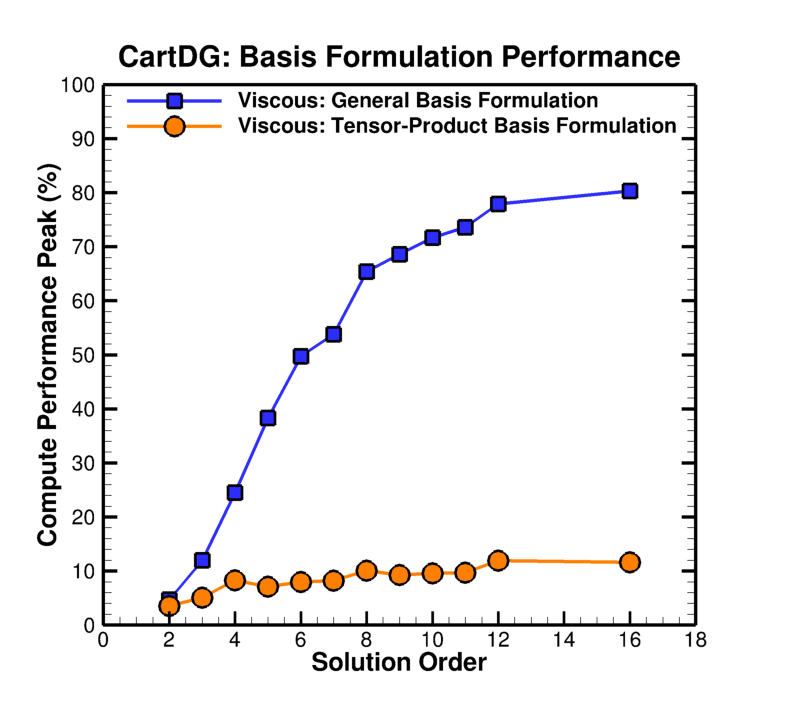
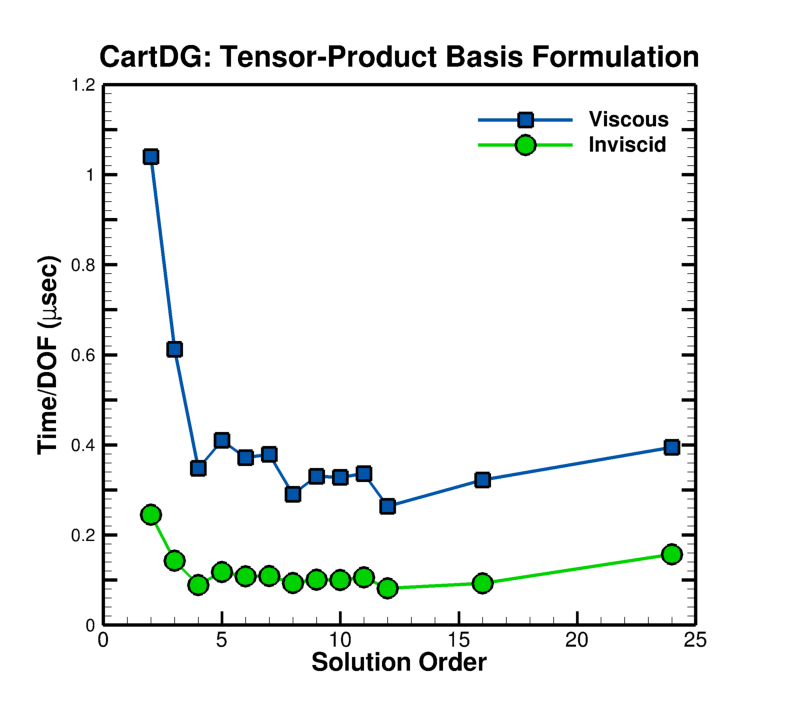
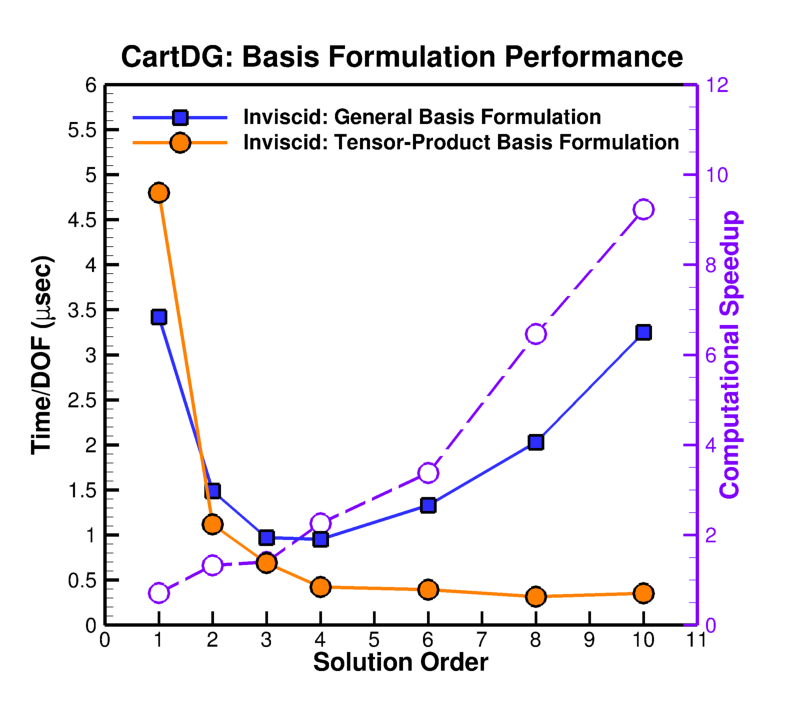
To demonstrate the computational efficiency of CartDG, several performance statistics for a wide range of orders of solution accuracy are provided. The sustained peak performance of the inviscid and viscous residual evaluations is shown below on an Intel Core i7-5960X Haswell-E processor with eight CPU cores, clock speed of 3.0 GHz, 4 GB of memory per core, and a theoretical peak performance of 384 GFLOPS (TauBench benchmark 5.25 seconds). The tensor-product DG formulation achieves roughly 12% sustained compute peak performance for evaluation of the residual of the compressible Navier–Stokes equations (viscous residual) at high solution orders of accuracy.

Left: Sustained peak performance of CartDG for tensor-product basis formulations of viscous and inviscid equations for 2nd-16th order accuracy. Right: Sustained peak performance for tensor-product basis and general basis formulations of the Compressible Navier–Stokes Equations for 2nd-16th order accuracy. The general formulation operations are casted as Level 3 BLAS matrix–matrix products.

Time per degree-of-freedom of CartDG for viscous and inviscid equations for discretization orders of accuracy ranging from 2nd- to 24th-order (lower values are better). Comparison between the tensor-product and general formulations are shown, noting the former being nearly 10x faster at high orders of accuracy.